跳转至

飞镖误差分析

问题描述

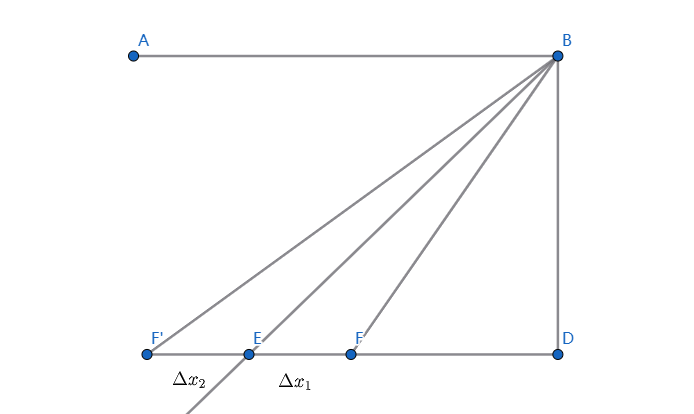
image-20250831172939133

如图为飞镖发射架简图，\(E\)点为底盘滑块中心点。射线\(BE\)为飞镖出射理想路径在底盘平面上的投影。已知\(BD=m\)，\(ED=n\)，假设\(BD\)平行于长方形场地的长边缘\(HG\)。

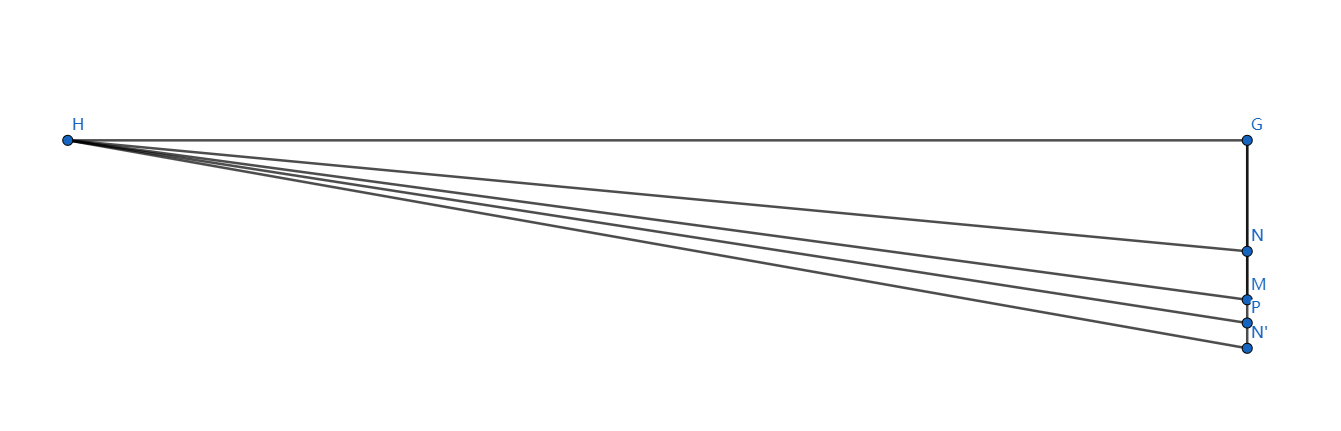
image-20250831180938669

如图为场地简图（发射架向左偏离时的情况），\(H\)为飞镖出射点，\(M\)为基地装甲模块轨道中心点，\(N\)和\(N'\)分别为基地装甲模块轨道的左端点和右端点。现在已知\(GM=a\)，\(MN=MN'=b\)，且\(\angle GHM=\beta\)

如果\(E\)点实际位置向右偏离至\(F\)点，或向左偏离至\(F'\)点，相应误差为\(EF=\Delta x_1\)和\(EF'=\Delta x_2\)，忽略飞镖飞行时产生的水平误差，并假设飞镖一定落在基地装甲模块移动轨道所在直线\(BD\)上，设落点为\(P\)点，分别求向左偏离和向右偏离时实际打击点的平面位置和目标打击点的平面位置之间的距离\(\Delta d_1\)和\(\Delta d_2\)。

误差分析

先分析\(\Delta d_1\)。

对于飞镖发射架，设\(\angle EBF=\alpha\)，在\(\triangle BEF\)中根据正弦定理有

\[ \dfrac{\Delta x_1}{\sin \alpha}=\dfrac{BF}{\sin \angle BED}=\dfrac{\sqrt{m^2+(n-\Delta x_1)^2}}{\sin\left(\arctan \dfrac{m}{n}\right)} \]

所以

\[ \alpha = \arcsin\left(\dfrac{\Delta x_1\sin\left(\arctan \dfrac{m}{n}\right)}{\sqrt{m^2+(n-\Delta x_1)^2}}\right) \]

即飞镖相对\(HM\)以\(\alpha\)角出射

对于场地，容易得到\(HM=\dfrac{a}{\sin \beta}\)，且\(\angle PHM = \alpha\)（因为发射架\(E\)点向右偏离，所以\(P\)一定在\(M\)左侧），\(\Delta d_1 = PM\)

在\(\triangle PHM\)中，根据正弦定理有

\[ \dfrac{PM}{\sin \angle PHM}=\dfrac{HM}{\sin \angle HPM} = \dfrac{a}{\sin\beta\sin \angle HPG}=\dfrac{a}{\sin\beta\cos (\alpha+\beta)} \]

所以有

\[ \Delta d_1=PM=\dfrac{a\sin\alpha}{\sin\beta\cos (\alpha+\beta)} \]

对于\(\Delta d_2\)，设\(\angle EBF'=\alpha'\)同理可得

\[ \alpha' = \arcsin\left(\dfrac{\Delta x_2\sin\left(\arctan \dfrac{m}{n}\right)}{\sqrt{m^2+(n+\Delta x_2)^2}}\right) \]
\[ \Delta d_2=PM=\dfrac{a\sin\alpha'}{\sin\beta\cos(\alpha'+\beta)} \]

很显然\(\alpha'<\alpha\)，所以发射架向左偏离同样的距离，比向右偏离误差更小。

数值验证

通过规则手册中的场地图纸和飞镖底盘图纸参数测量，得到实际参数如下（所有长度单位均为mm）：

1
m = 428 a = 3225 beta = 7.7°

同时通过规则手册得知单个装甲模块的宽度为140mm，为了确保准确击中，这里要求误差不能超过半个装甲模块的宽度，即70mm

因为计算量非常大，我用matlab画了这两个方程的解空间构成的曲面图，图中曲面上的红线为70mm：

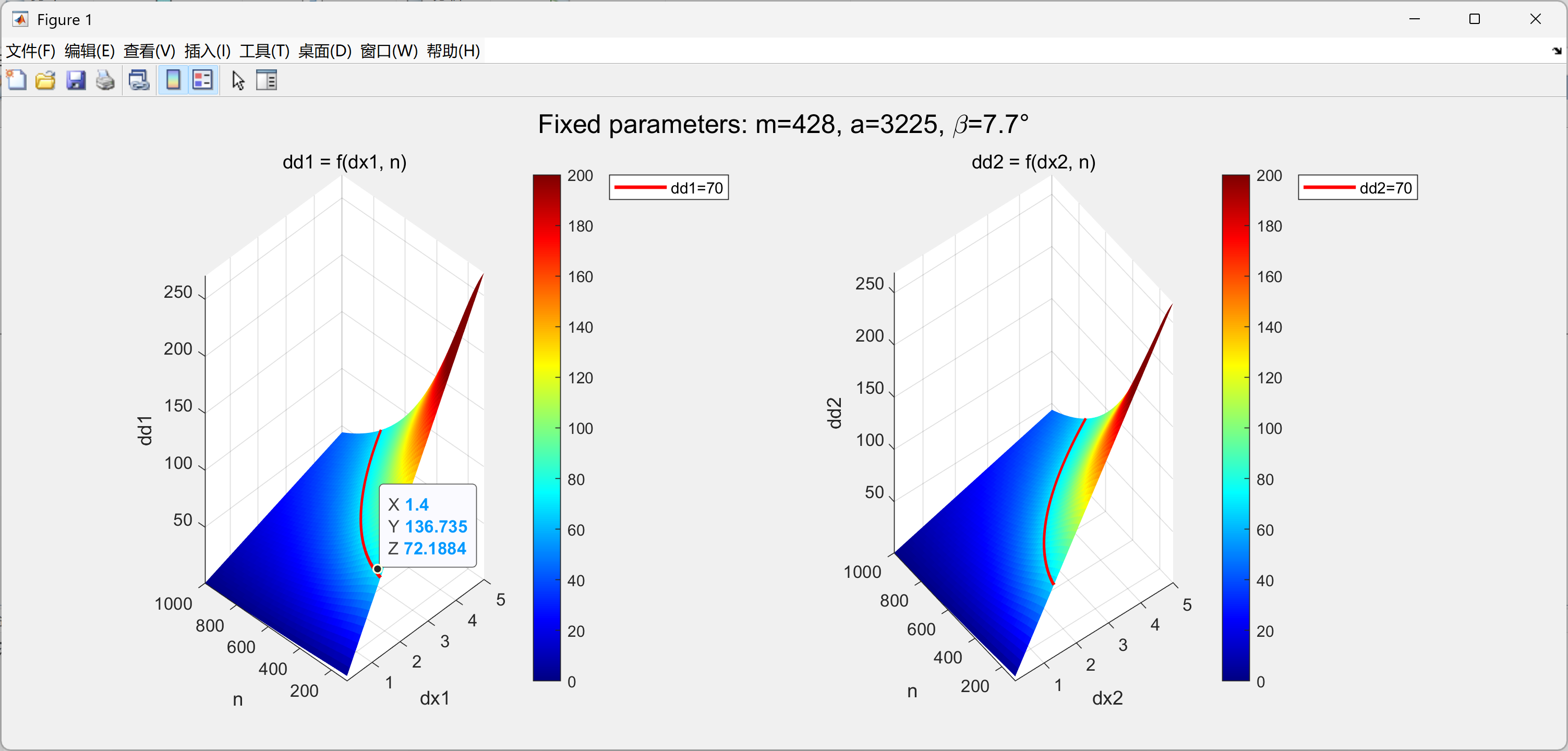
image-20250831191355755

很明显，只要\(\Delta x_1\)和\(\Delta x_2\)小于1.4mm左右，就能保证yaw轴方向的误差在可控范围内。

附：对应的MATLAB绘图代码 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
clear;
clc;

m = 428;
a = 3225;
beta_deg = 7.7;
beta = deg2rad(beta_deg);

dx_range = linspace(0.1, 5, 50);
n_range = linspace(100, 1000, 50);
[DX, N] = meshgrid(dx_range, n_range);

DD1 = zeros(size(DX));
DD2 = zeros(size(DX));

for i = 1:size(DX, 1)
    for j = 1:size(DX, 2)
        % 计算 dd1
        dx1 = DX(i,j);
        n_val = N(i,j);
        if abs(n_val - dx1) < 1e-3
            DD1(i,j) = NaN;
        else
            sin_atan = sin(atan(m / n_val));
            deno1 = sqrt(m^2 + (n_val - dx1)^2);
            alpha = asin((dx1 * sin_atan) / deno1);
            DD1(i,j) = (a * sin(alpha)) / (sin(beta) * cos(alpha + beta));
        end

        % 计算 dd2
        dx2 = DX(i,j);
        deno2 = sqrt(m^2 + (n_val + dx2)^2);
        alpha_p = asin((dx2 * sin_atan) / deno2);
        DD2(i,j) = (a * sin(alpha_p)) / (sin(beta) * cos(alpha_p + beta));
    end
end
figure('Position', [100, 100, 1200, 500]);
subplot(1,2,1);
surf(DX, N, DD1, 'EdgeColor', 'none');
hold on;
contour3(DX, N, DD1, [70 70], 'r', 'LineWidth', 2); % 等高线
[~, h] = contour3(DX, N, DD1, [70 70], 'r', 'LineWidth', 2);
hold off;
title('dd1 = f(dx1, n)');
xlabel('dx1');
ylabel('n');
zlabel('dd1');
colorbar;
colormap jet;
clim([0 200]);
view(3);
legend(h, 'dd1=70');
subplot(1,2,2);
surf(DX, N, DD2, 'EdgeColor', 'none');
hold on;
contour3(DX, N, DD2, [70 70], 'r', 'LineWidth', 2); % 等高线
[~, h] = contour3(DX, N, DD2, [70 70], 'r', 'LineWidth', 2);
hold off;

title('dd2 = f(dx2, n)');
xlabel('dx2');
ylabel('n');
zlabel('dd2');
colorbar;
colormap jet;
clim([0 200]);
view(3);
legend(h, 'dd2=70');
sgtitle(['Fixed parameters: m=', num2str(m), ', a=', num2str(a), ', \beta=', num2str(beta_deg), '°']);